Loe raamatut: «Все науки. №12, 2024. Международный научный журнал»

Ибратжон Хатамович Алиев, G’olibjon Qo’ldashov, Sultonali Abdurakhmonov, Jamolitdin Abdullayev, Умиджон РустамовErkinjon XolmatovNurmakhamad JurayevMamatisa JalilovШавкатжон Самитдинович СайитовЗарифа Мукаддамовна КабироваФазилат Одилжон кизи ЮлдашеваИнтизар Батырбековна БекимбетоваШахло Акмалжон кизи ИброхимоваХожимурод НосировЖамшидбек Соибжонович НематжоновХусанбой НематовБаходир Солиевич Казаков ja teised

Font:

Авторы: Алиев Ибратжон Хатамович, Qo’ldashov G’olibjon, Abdurakhmonov Sultonali, Abdullayev Jamolitdin, Рустамов Умиджон, Xolmatov Erkinjon, Jurayev Nurmakhamad, Jalilov Mamatisa, Сайитов Шавкатжон Самитдинович, Кабирова Зарифа Мукаддамовна, Юлдашева Фазилат Одилжон кизи, Бекимбетова Интизар Батырбековна, Иброхимова Шахло Акмалжон кизи, Носиров Хожимурод, Нематжонов Жамшидбек Соибжонович, Нематов Хусанбой, Казаков Баходир Солиевич

Главный редактор, Директор НИИ "ФРЯР" Ибратжон Хатамович Алиев

Научный директор Боходир Хошимович Каримов

Технический директор Султонали Мукарамович Абдурахмонов

Экономический директор Ботирали Рустамович Жалолов

Заместитель главного редактора Миродилжон Хомуджонович Баратов

Редактор Гулчехра Ғуламжановна Ғаффарова

Иллюстратор Ибратжон Хатамович Алиев

Иллюстратор Фарходжон Анваржонович Иброхимов

Дизайнер обложки Раънохон Мукарамовна Алиева

Корректор Гулноза Мухтаровна Собирова

Корректор Дилноза Орзиқуловна Норбоева

Модератор Фарходжон Анваржонович Иброхимов

ISBN 978-5-0067-1692-6 (т. 12)

ISBN 978-5-0065-0531-5

Создано в интеллектуальной издательской системе Ridero

ФИЗИКО-МАТЕМАТИЧЕСКИЕ НАУКИ

On The Evolutionary Change In The Power Of Solar Radiation On Earth Over Time

UDK: 530.1

Ibratjon Aliyev¹, G’olibjon Qo’ldashov², Sultonali Abdurakhmonov³, Jamolitdin Abdullaev⁴

¹SRI «PRNR», Electron Laboratory LLC, 151100, Republic of Uzbekistan, Ferghana region, Margilan
²National Research Institute of «Renewable Energy Sources» under the Ministry of Energy of the Republic of Uzbekistan, 100000, Republic of Uzbekistan, Tashkent region, Tashkent
³Fergana Polytechnic Institute, 150100, Republic of Uzbekistan, Fergana region, Fergana

⁴Fergana branch of Tashkent University of Information Technologies named after Mukhammad al-Khwarizmi, 150118, Republic of Uzbekistan, Fergana region, Fergana, Mustaqillik street, 185

Abstract. This study presents the process of theoretical modeling of the current value of the solar radiation energy by means of the Laplace equation, taking the Sun as a radiating object with the setting of appropriate boundary conditions in a spherical coordinate system. For the obtained solution of the equation, through the use of dynamic modeling and time dependence, taking into account thermonuclear processes in the Sun, the method of separation of variables is used. As a result of the study, the function and its graphs are presented, which allow us to observe the indicators of radiated power per square meter of the surface of the planet Earth.

Keywords: Laplace equation, method of separation of variables, thermonuclear fusion, solar radiation.

Аннотация. В данном исследовании представлен процесс теоретического моделирования текущего значения энергии солнечного излучения с помощью уравнения Лапласа, в котором Солнце рассматривается как излучающий объект с заданием соответствующих граничных условий в сферической системе координат. Для полученного решения уравнения, благодаря использованию динамического моделирования и временной зависимости, с учетом термоядерных процессов на Солнце, используется метод разделения переменных. В результате исследования представлены функция и ее графики, которые позволяют наблюдать показатели излучаемой мощности на квадратный метр поверхности планеты Земля.

Ключевые слова: уравнение Лапласа, метод разделения переменных, термоядерный синтез, солнечное излучение.

Introduction

The development of energy and especially solar energy at the moment creates the need for a full-fledged mathematical model capable of determining, in the dynamic case, in the selected coordinate system, the amount of radiation power directed from the Sun to any of the specified coordinates. This simulation will allow you to determine the amount of power at a specified point on Earth at any given time period. However, in order to create a connection between this pattern and the dynamic characteristics of the described system, it is necessary to determine the rate of expenditure of hydrogen fuel from the Sun, taking into account all known characteristics.

At the moment, it is known that when extrapolating, based on data obtained from probes, including Voyagers, the Sun generates radiation equivalent to 4 million tons of matter at the time of 4.5 billion. The magnitude of the solar constant equal to 1,360.8 W/m2 up to the atmosphere has been established for the years of the star’s existence [1—3; 10—11]. Based on the current model of star formation and the model of mass expenditure, the value is clearly formed that at the time of 5.6 billion years after the formation of the star, the radiation power will increase by 11% and amount to 1,532.47 W/m2, respectively [4; 6—7]. The resulting value may be sufficient to transform the model into a dynamic form.

For further modeling, we will take an equation capable of describing the phenomenon of radiation in the presence of radiation, with the condition that in this case no energy is supplied to the source from the outside or, in comparison with the values of solar radiation, the power of cosmic radiation can be ignored, which is demonstrated in practice. Despite the fact that even taking into account the presence of not a small number of sources of cosmic radiation, the percentage of radiation – the flux of charged particles, even compared with the solar neutrino and the flux of solar charged particles, is extremely small in percentage [5; 7—10]. Based on this, the main radiation energy is transmitted by photonic radiation.

In many works, the processes of radiation formation in the Sun and the process of energy transfer from the Sun to other planets, including to Earth, are considered, but the proposed technology for mathematical analysis of available data and the development of further radiation processes are not considered. Therefore, this study is relevant.

Materials and methods of research

To carry out the research, empirical materials that are well-known, relevant literature on the topic, as well as data obtained from international research papers were used [13—15; 18—19]. Numerous probes have been launched to measure the radiated energy, with the help of which radiation parameters are periodically studied. Within the framework of the ongoing research, methods of theoretical modelling, analysis, classification, the method of separation of variables (Fourier method), the method of using differential equations for modelling, with the resulting methods for determining their solutions, are applied.

Research

At the moment, a dynamic problem has been formed with respect to the Laplace equation (1), with respect to the function (2), with known initial conditions (3—4), proceeding from the phenomenon of thermonuclear fusion.

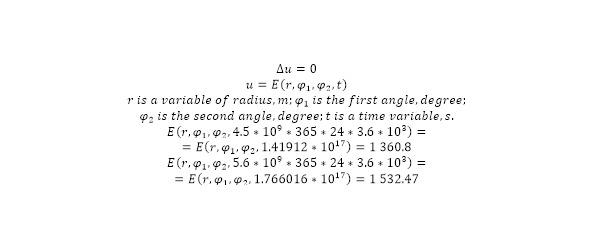
To determine the boundary conditions, it is sufficient to adopt a spherical coordinate system, despite the fact that the coordinate at zero angles at a radius of 1 astronomical unit is the position of the planet Earth on New Year’s Day – the transition from the night of December 31 to January 1. The Sun is also accepted as an absolutely smooth body, spreading uniform radiation over the entire surface, due to which an error for the presence of black spots is initially stipulated, which can be eliminated later. Thus, based on the above, it is necessary to state the fact that, based on the conditions taken, the Earth is located at 0 degrees in the latitude angle of the Sun, also taking into account the deviation of 23.497 degrees of the Earth’s axis, while the maximum deviation to the poles of the planet in the form of the specified angle can be calculated.

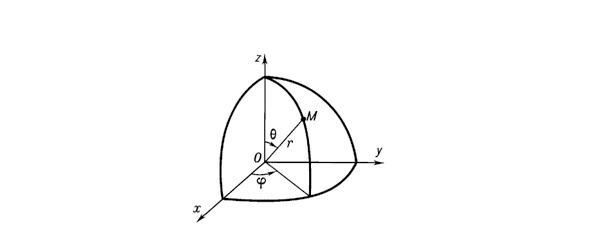
Fig. 1. Spherical coordinate system

The conditions set lead to the fact that between the center of the Sun, the Earth and one of the poles of the Earth there are 3 imaginary straight lines forming at the time of the vernal equinox a right triangle with legs of 1 astronomical unit (1,496*108 km) and 1 radius of the Earth (for the polar case 6,356.8 km and for the equatorial 6,378.1 km), from where it is possible to calculate the angle according to the Pythagorean theorem (5).

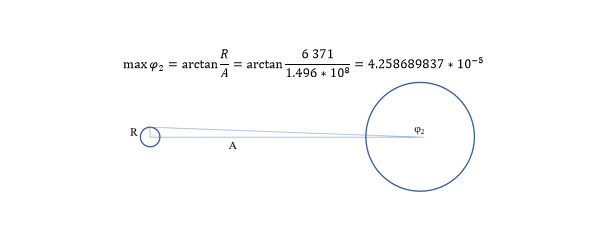
Fig. 2. The modeling schemes

Also, from the same ratio, but in a transformed form, it is possible to obtain the angle of deviation at the time of June 21 and December 21 according to the cosine theorem (6—9).

Similar calculations are used to determine the boundary conditions with respect to the angle of longitude (10—13).

Based on certain data, it is possible to state the change of function (2) to (14) and the problem of the following boundary conditions (15—18), given that the boundary conditions and the dynamic phenomenon are known, the Fourier method of variable separation can be adopted as a solution for it.

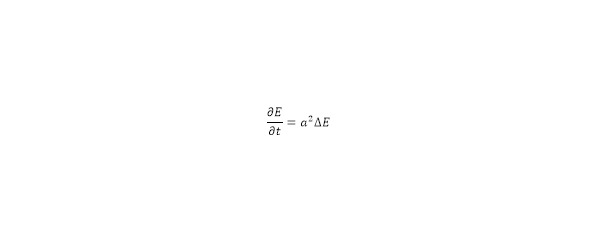
Now that the initial and boundary conditions, as well as the corresponding equation, have been determined at the specified moment, it is necessary to pay attention to the effect of the Laplace equation in static form, and it, as a partial equation from the Helmholtz equation, can be interpreted as follows. Namely, for the reason that in this case the phenomenon of energy transfer is observed, and in this case the Laplace equation is used to display in a global sense a model of an emitter or an energy-emitting «charge» in the face of the Sun. Thus, on a more local scale, the harmonic function taken will satisfy, based on these conditions, the homogeneous equation of thermal conductivity or energy conductivity (19), including based on the transformation model for the connection of the Helmholtz equation and the wave equation.

Where, the coefficient of energy conductivity is determined in (20), along with all the determined parameters, including the coefficients of energy conductivity of the vacuum between the Sun and the Earth (21), the specific energy capacity (22) and the available energy density under the circumstances in the specified area (23).

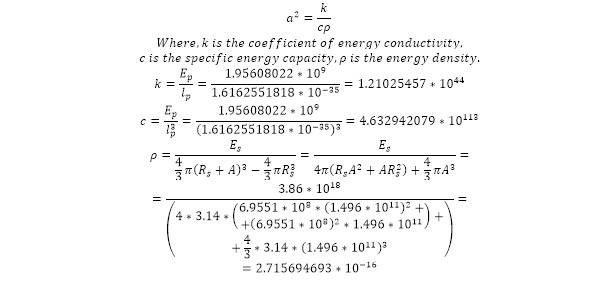
Based on the calculated parameters according to (21—23), expression (20) obtains a numerical indicator (24).

Based on the conditions obtained, it is possible to determine that the problem can be solved by taking the form of an equation of the form (25), where, after substitution, a transformation can be obtained according to (26), with an equated coefficient (27).

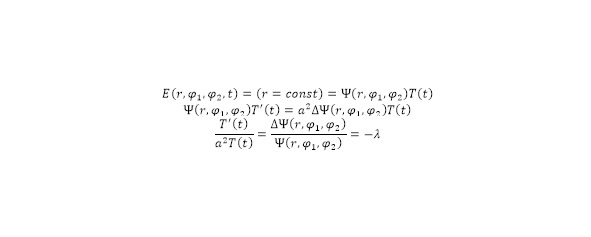
From expression (27), 2 partial differential equations are formed – 1 ordinary with respect to time in the first degree and the second in the square of partial derivatives. The first equation is solved by adopting a general solution with an exponential form, where, after substitution, a characteristic form is presented, from which a general form of the function is formed – the solution of the resulting ordinary differential equation in time (28).

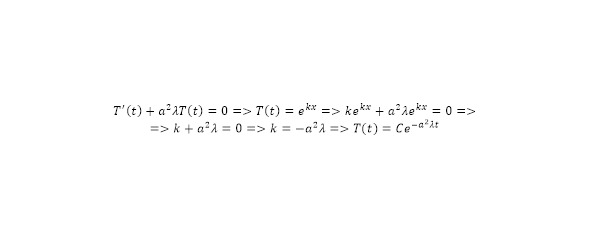
With respect to time, initial conditions (3—4) have already been obtained, which can be substituted to form initially the coefficient value from (27) to (29), the independent variable in (30) and the resulting form of a function with known constants in (31).

The resulting function is the solution of only one differential equation, the second (32) is formed relative to the Laplacian in a spherical coordinate system with a known constant.

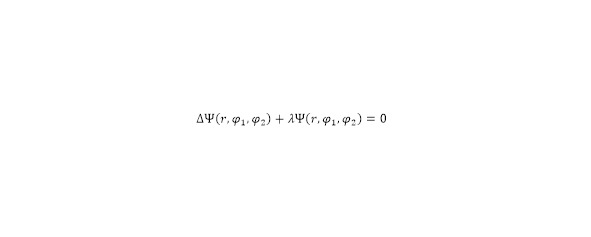
The solution of this equation is presented initially after the disclosure of the Laplacian for the Ψ-function in a spherical coordinate system, where the Fourier variable separation method is applied, which was originally applied in (26). Then subsequently, after substitution, the resulting separation expression is revealed, forming separate groups of derivatives in the specified system (33).

Taking into account the resulting transformation and taking into account the transformation of the original ratio, the Laplacian ratio of the function and the function itself can be substituted into the transformed form after separating the variables, from which a separate additional ratio is created for each function – radius, first and second angles, as well as for the second derivatives of these expressions (34).

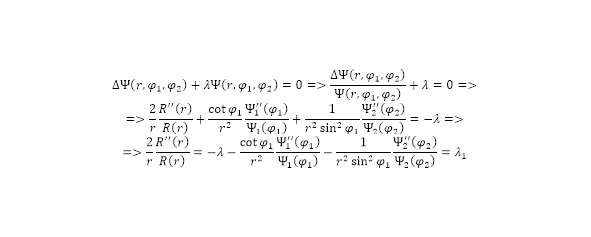
From the first ratio in (34), a second-order differential equation with respect to radius is formed, which can be solved after revealing the ratio and using the integral of the second degree with respect to the radius variable in the second degree. When integrating in both directions, in the right case, a known ratio is obtained, in the left case, the function itself is used as a variable, which allows us to arrive at the resulting equation between the value of the function and the variable of the radius of this function.

Transformations with respect to double logarithm, followed by further exponentiation after transformations and repeated logarithm in kind, allow us to arrive at a function relation that becomes complete after being reduced in an algebraic transformation (35)

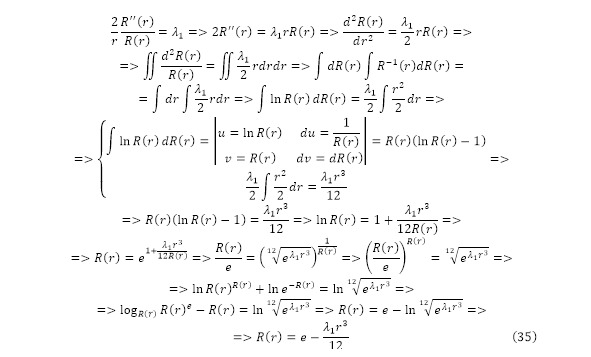
Taking into account the obtained type of function, as well as the known ratio, it can be noted that in (34) an additional second coefficient was introduced, which took part in (35) and the resulting formula of the radius function. The value of this coefficient can be calculated based on the appropriate type of function, taking into account the fact that the radius is a constant equal to a single astronomical unit, calculations become the simplest and most definite (36).

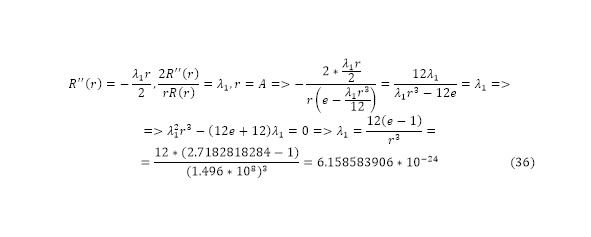
Thus, the function from (35), taking into account the value of the coefficient (36), takes the form (37) with a single value of the function at a given radius in (38).

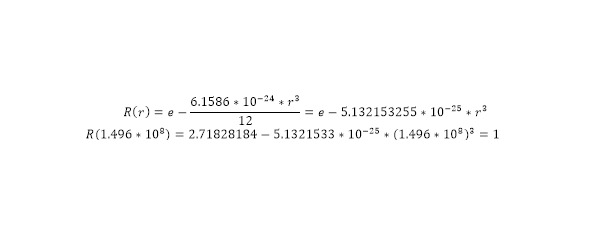
Since the type and value of the radius function has been determined, the ratio in (35—36) can be used later to operate with the function of the first angle from a given spherical coordinate system. After converting the ratio, a third additional coefficient is introduced, from which, consequently, a new ordinary differential equation of the second degree is created using trigonometric functions. Subsequently, after the transformation, the operation of integration, exponentiation, logarithmization and transformations with logarithms, which were carried out within the framework of calculations in (35), are applied to the function of the first angle using the general form of this function (39).

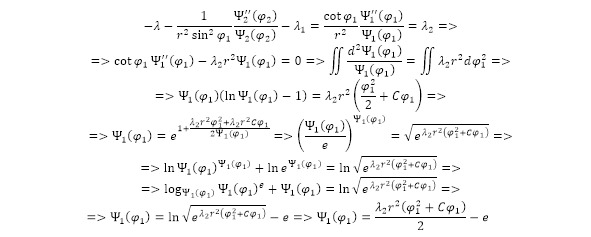
With respect to the obtained function of the first angle in the spherical coordinate system, which also depends on the independent constant and the introduced constant, there are also boundary conditions derived from the available empirical data (18). The application of each of them creates 3 forms of the function with the specified values of the angle variable and the value of the function as a whole, while the third form causes the variable to be replaced in the first and further transition from a system with 3 equations to 2 equations, and then, after deducing the function for the independent constant into a single equation. The expression formed in this way, after elementary algebraic transformations, leads to the value of the introduced third coefficient (40), its substitution into the formula of the independent constant (41), which can be substituted into the form of a function (42).

As a result, a uniform form with constants for the first function is obtained, on the basis of which it is possible to continue the given ratio with transformation into the form of an ordinary differential equation of the second degree relative to the second angle. The solution is carried out after the conversion of the function, where all 3 specified constants are enclosed, which are used during the conversion. During the double integration on the left side, due to the fact that the first angle is used as a variable in the square of the sine, double integration relative to the second angle cannot be performed in principle, which is why the first and second independent coefficients appear.

Thus, a relation is created with respect to which natural logarithm is performed, which, after appropriate algebraic operations, leads to a single form of the function with respect to the second angle (43).

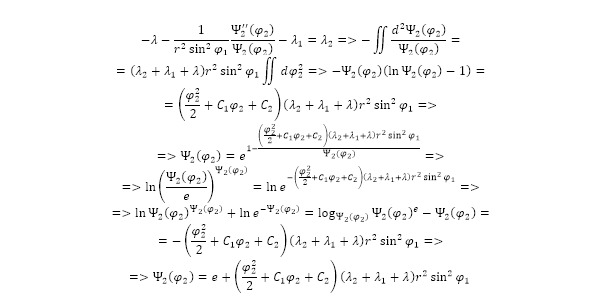
Based on the experimental data in (15—17) [1—5; 13—17; 19], boundary conditions can be used [17—19] and, consequently, 3 equations for the second angle, each of which is solvable after converting the third equation and reducing to 2 equations. After applying the substitution method, a single equation is output for the system of equations, after which the value for the first coefficient is calculated, as well as the square of the sine of the first angle relative to the specified boundary conditions, which can then be used in the substitution method, creating a single form of the equation (44).

As a result of the calculations, the function has already been determined in time, the first and second corners, taking into account that the value of the function in radius is equal to one, the general appearance of the function looks according to (45).

The resulting function can describe the energy value taking into account the empirical coefficient, so that a graph of the function (45) can be presented. It is important to note that the function depends on 3 variables – the first and second angles, as well as time, which can be represented as an animation, as well as by a single time.

Results

In this case, the graph is plotted relative to each angle and shape relative to a given time of 4.5 billion. years after the formation of the Sun, which is also used in a given function (Fig. 1—2).

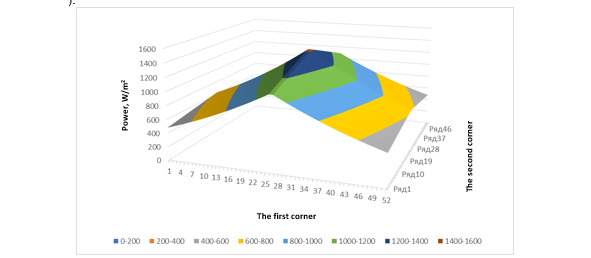
Fig. 1. The first perspective of the constructed three-dimensional graph at the time of 4.5 billion years after the formation of the Sun

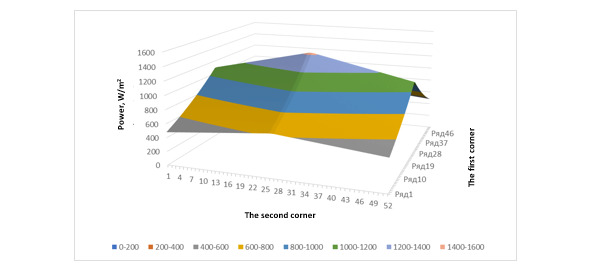
Fig. 2. The second perspective of the constructed three-dimensional graph at the time of 4.5 billion years after the formation of the Sun

A similar method leads to the formation of graphsrelative to 5.6 billion. years (Fig. 3—4).

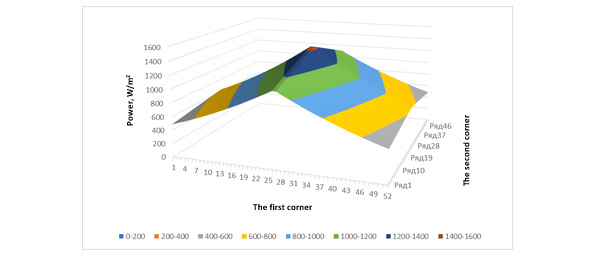
Fig. 3. The first perspective of the constructed three-dimensional graph at the time of 5.6 billion. years after the birth of the Sun

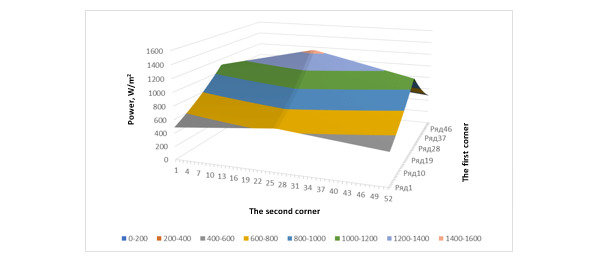
Fig. 4. The first perspective of the constructed three-dimensional graph at the time of 5.6 billion. years after the birth of the Sun

The analysis of the presented three-dimensional graphs indicates that the maximum value of solar radiation energy increases over time. The coverage of the high-energy region of the earth is relatively increasing over time. But, if we take the time value used, the effect of changing the energy of solar radiation can be considered insignificant (within 1 billion the change in years was about 7.46%). As a result, a resulting graph is obtained describing the power of energy over time, taking into account radioactive phenomena in the Sun, as well as in any illuminated coordinate on the Earth’s surface.